I have created a 45-bit segment display for Hangul, the Korean script. See the live demo here.
What is Hangul?
Recently, I have started to learn a bit of Korean. One of the most fascinating parts of the language is its script called 한글, or Hangul in its romanized form.
This language, like the Latin script, allows you to pronounce each word by reading the letters left to right. In Korean, however, each “block” represents a syllable block, which contains all the jamo (symbols) that are used in the syllable.
For example, the ㅂ represents a p or b, the ㅏ represents an a and the ㄴ represents an n. So a character like 바 creates the syllable ba, and the character 나 creates the syllable na. So 바나나 represents ba-na-na, which is actually the word for banana in Korean!
As Professor Emeritus of Korean language and linguistics Jaehoon Yeon writes in their book Beginners' Korean (ISBN 978-1-399-82161-2), “Hangeul is one of the world's most scientific writing systems and has received worldwide acclaim from countless linguists. As a unique systematized phonetic script, Hangeul can express up to 10,000 sounds. It is perhaps the most outstanding scientific and cultural achievement of the Korean nation.” While I think it may be a stretched brag to call the syllables “sounds”, it is amazing how such a systematized script can display so many syllables as unique characters.
To practice and to get to know them, I have tried to learn the script in my own way!
What are segment displays?
A segment display uses segments instead of pixels to create text on screen. The most common example is the 7-bit segment display used to display numbers.
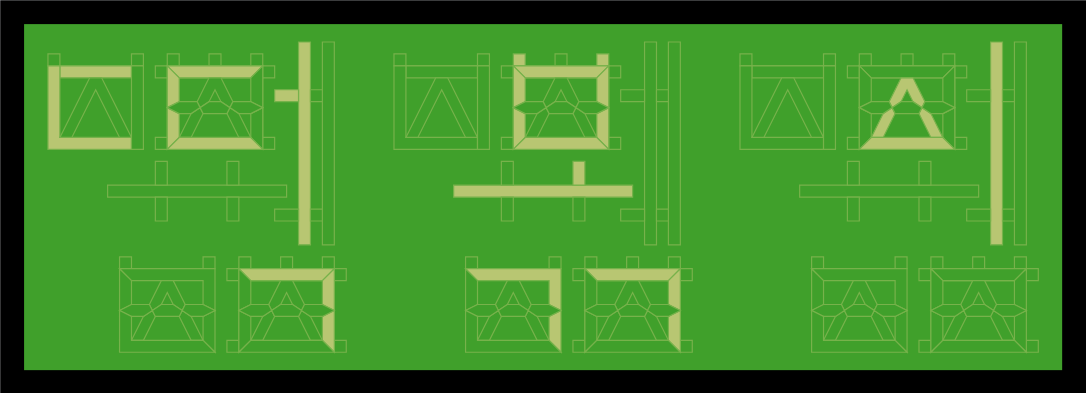
However, as the Korean Wikipedia page on segment displays reveals, such segment displays aren't very good at displaying Korean characters. For example, can you decipher what is written in this image?

I've recently learned to read Korean, and decided to design a segment display that would properly show Hangul in an unambiguous and readable format. In my opinion, the result looks readable to a degree where it could pass as a peculiar font!
The challenge with segment displays is to use as few segments as possible to create a readable font. In my situation, I have created a 45-bit design, which means that the design uses 45 segments to create the font. In other words, all Hangul syllable blocks can be displayed on my design by activating a unique group of segments.
How the design was made
Creating the design consisted of three parts:
- Designing the individual segments
- Designing the font
- Building the demo
Desigining the individual segments
Most of my design has based itself around this public domain Hangul romanization guide. It contains a comprehensive explanation of all possible characters in the Hangul script:
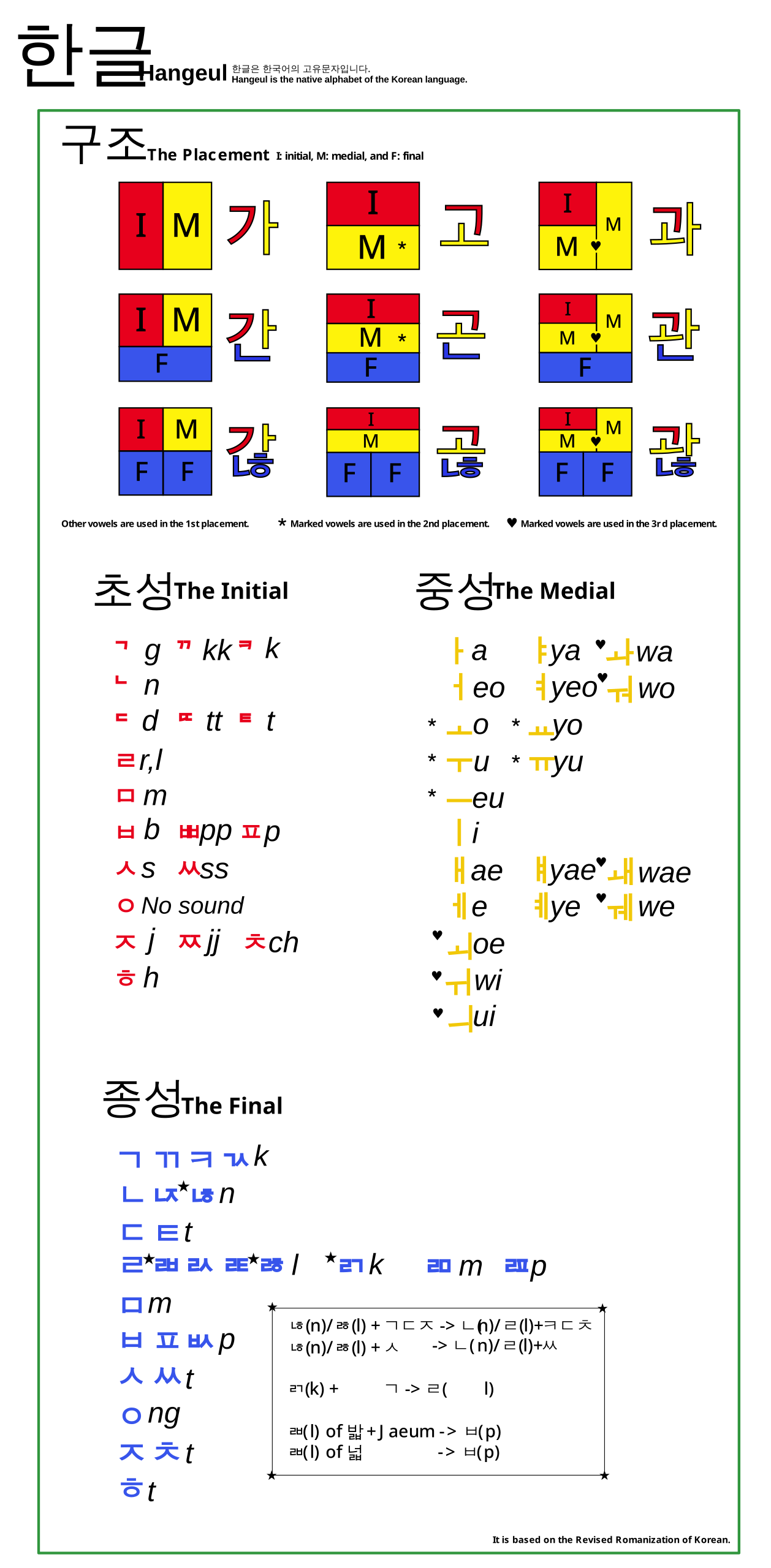
As you can see, every syllable block consists or 2 or 3 jamo, and they are rendered independently of one another – only the placement can change. This means we can design the three parts (initial, medial, final) independently and then arrange them in an appropriate fashion.
Initial part
To make the creation of a segment display easier, I've taken the freedom to divide the consonants into two groups:
- The blocky jamo ㄱ, ㅋ, ㄴ, ㄷ, ㅌ, ㄹ, ㅁ, ㅂ, and ㅍ.
- The curvy jamo ㅅ, ㅇ, ㅈ, ㅊ and ㅎ.
The blocky jamo can be rendered by lighting the edges of a square: ㄱ highlights the top and the right edge, ㄴ highlights the left and the bottom edge, and ㅁ highlights all four edges. To add support for all blocky jamo, the square can have a bar in the middle for the jamo ㅋ and ㄹ, and the display can have some dots near the corners for the jamo ㅂ and ㅍ.
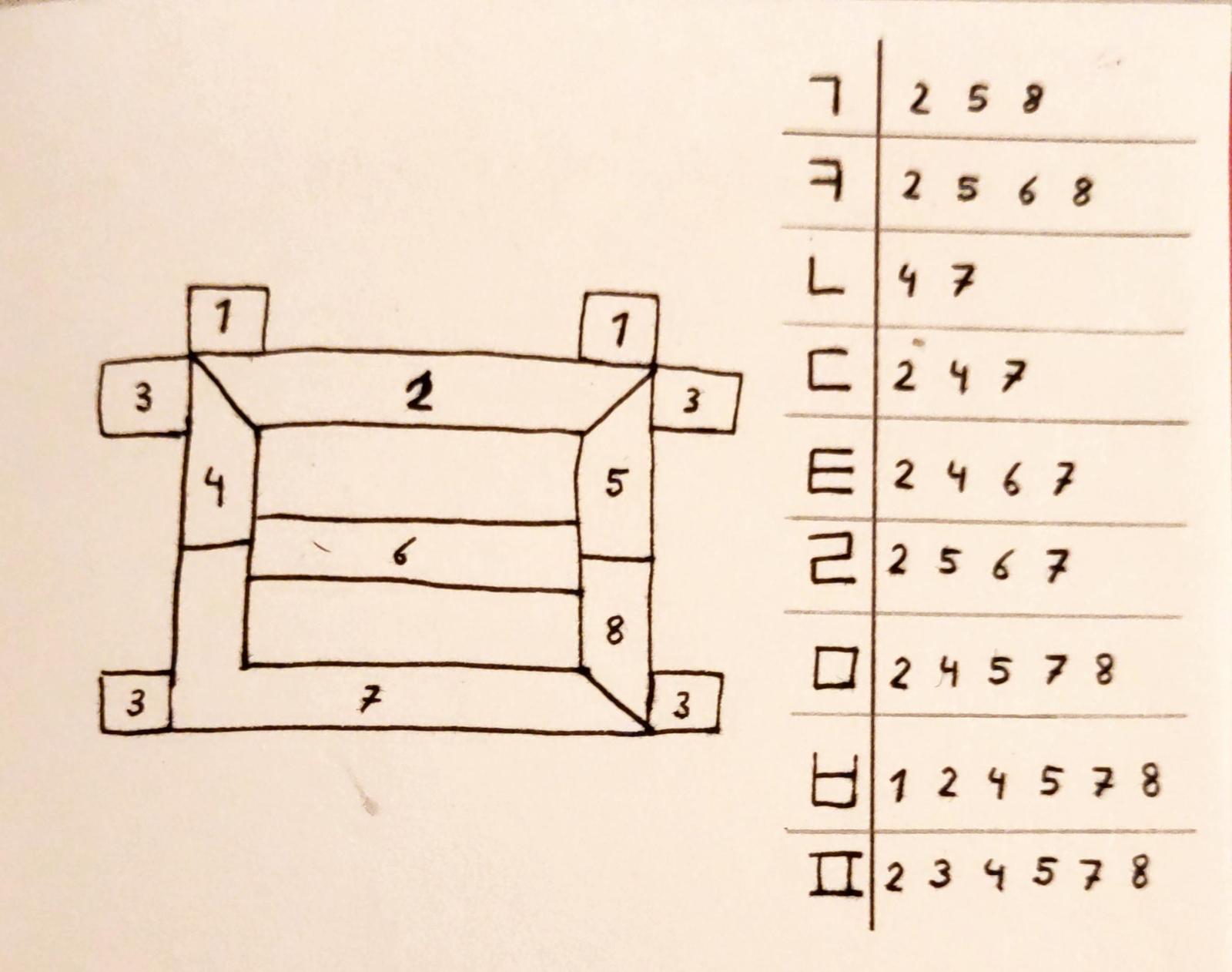
The curvy jamo are a bit more complex. By adding the ㅅ inside the square shape, one can automatically create ㅅ, ㅈ and ㅊ – but the circles in ㅇ and ㅎ form a problem. By compromising and making the circle a triangle, however, one can render ㅇ, and ㅎ with the addition of a final dot in at the middle of the top edge.
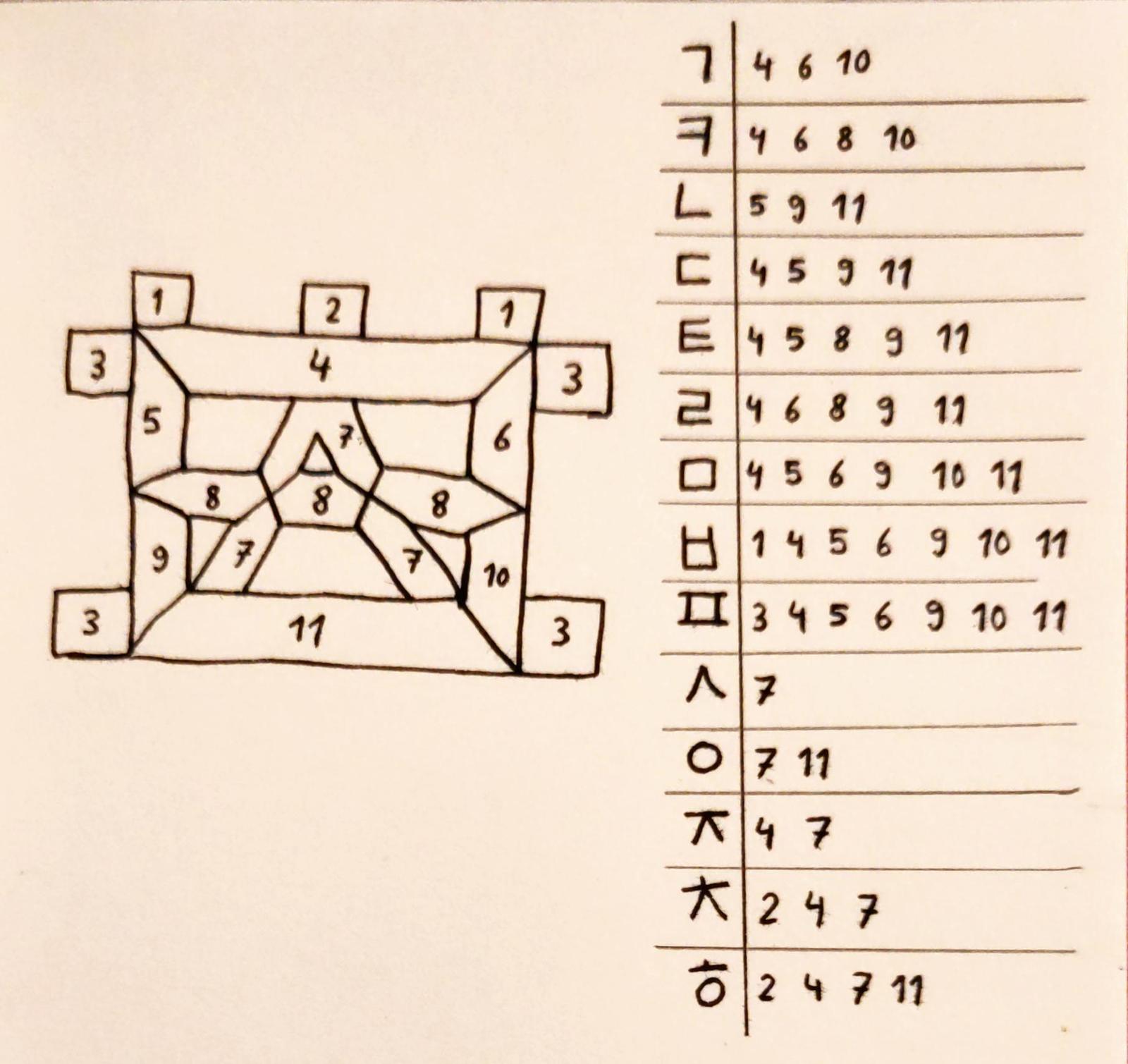
Some initial jamo are double – but these are only ㄱ, ㄷ, ㅂ, ㅅ, and ㅈ in their doubled form. By creating a second (but simplified) version of our initial segment display, we can create all possible initial characters.
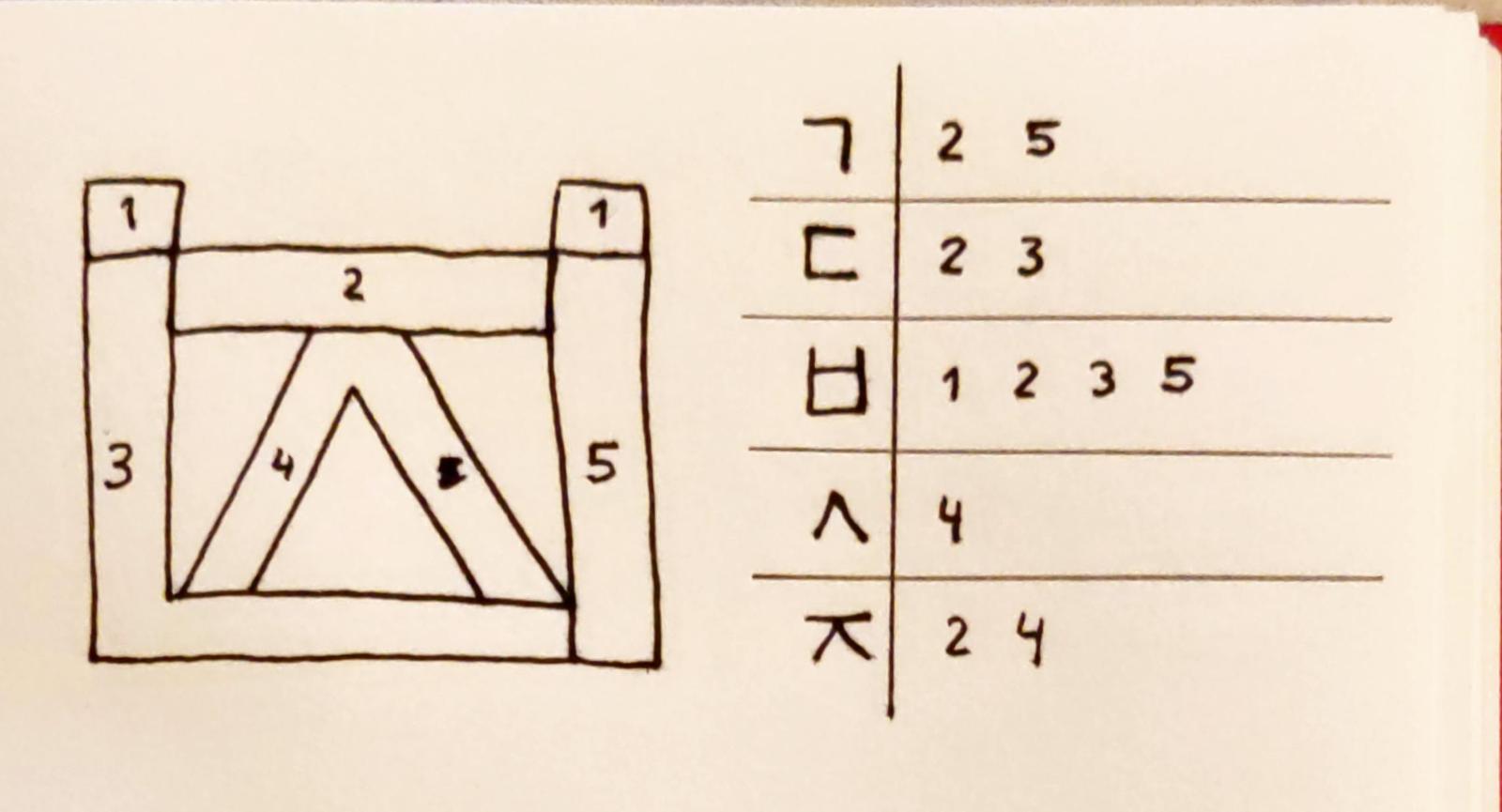
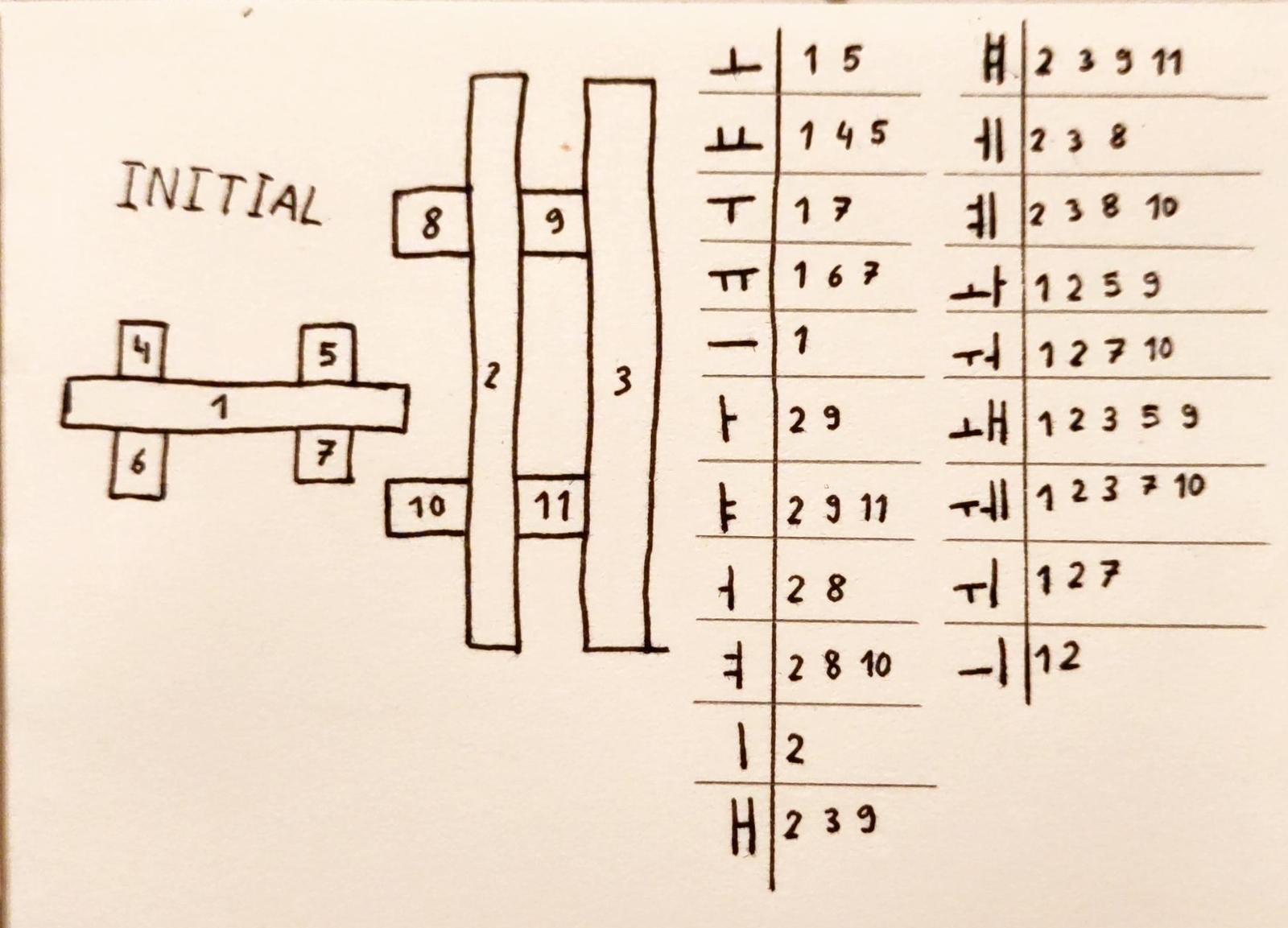
The medial part is always the only vowel in every syllable block. The available vowels are the following:
- The horizontal jamo ㅗ, ㅛ, ㅜ, ㅠ, and ㅡ.
- The vertical jamo ㅏ, ㅑ, ㅓ, ㅕ, ㅣ, ㅐ, ㅒ, ㅔ, and ㅖ.
- The combined jamo ㅘ, ㅝ, ㅙ, ㅞ, ㅚ, ㅟ, and ㅢ.
When combining it with a consonant jamo such as ㅇ, horizontal jamo render like 으, vertical jamo render like 이, and combined jamo render like 의. As you can see, every jamo's direction, shape and placement is decided by the long lines. Given that most combinations can exist, we can build two horizontal lines, two vertical lines, and then have some dots on most sides. One detail is that the dots on the vertical bar in ㅝ and ㅞ are supposed to go below the horizontal bar, so that is a detail to keep in mind. This brings us to the following design:
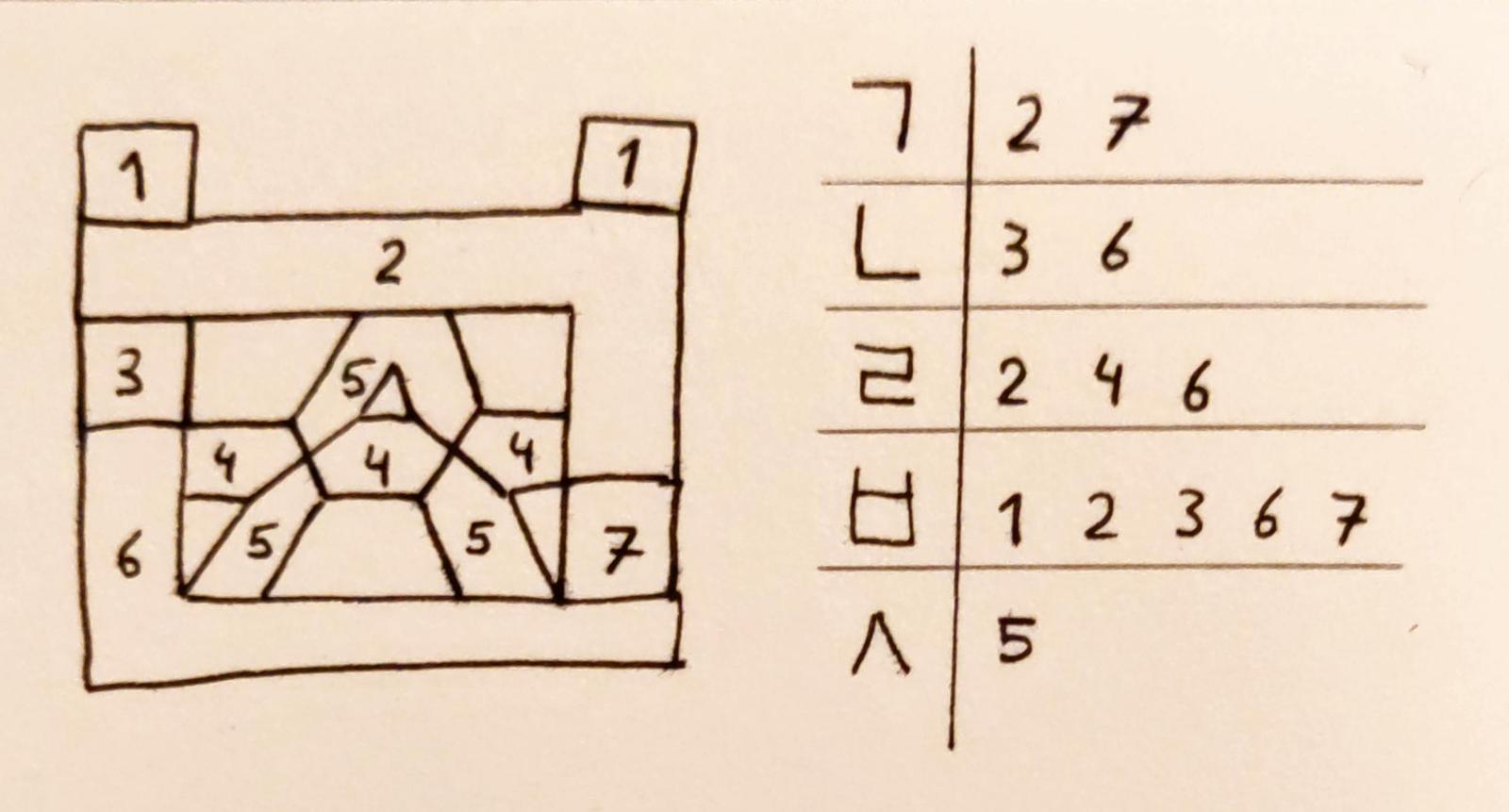
Final part
All consonant jamo appear in the initial part – so the design for the initial part is sufficient to render any jamo. However, the final part can consist of two jamo! More specficially, when rendering double jamo:
- The first jamo can be ㄱ, ㄴ, ㄹ, and ㅂ.
- The second jamo can be ㄱ, ㅅ, ㅈ, ㅎ, ㅂ, ㅌ, ㅁ and ㅍ.
So when creating two jamo segment displays, one should be able to render all consonant jamo, and the other should render a select group of jamo. The arrangement depends on how the syllable block is formed.
Designing the font
To design the font, we now have the knowledge of how we can render the initial, medial and final parts of the syllable block. The trick is to arrange the segments in a way that any rendered syllable block remains readable.
For the website's design, I have relied on a font from some ancient Korean sources, which would sometimes render the final part a bit to the side of the initial and medial parts. This would allow the syllable block be a bit oddly shaped but still retain consistency.
As such, whenever the final part renders only one jamo, it renders it in the second jamo, leaving the first jamo only to need to render ㄱ, ㄴ, ㄹ, ㅂ, and ㅅ when necessary.
Building the demo
While the design of the segment display is complete with this design, building a demo also requires the system to translate Korean text to a series of bits that activates the segments appropriately. For this, the blog post How Korean input methods work by m10k has proven extremely useful. This helped me write a Hangul parser that identifies the individual jamo in order to render them on the webpage.
With the use of Elm, I then transformed the script into a webpage that renders any inserted Korean text into a proper segment display. The website dynamically decodes the user input and renders the text on screen.
Despite the visual quirks—like some jamo (e.g., ㅅ, ㅇ) not rendering perfectly, or syllables like 이 appearing disproportionately small next to something like 쀲—the display manages to stay surprisingly readable. These trade-offs are part of keeping the design minimalistic. With more bits (segments), one could definitely improve clarity and consistency—especially in character size. I'd like to design a more advanced segment display based on the segment displays on the Berlin U-Bahn and the train stations in Brussels, which balance clarity and space beautifully.


Why doesn't this already exist?
Before designing my own segment display, I looked around the internet and couldn't find an existing segment display! I would love to hear from Koreans whether they ever encounter segment displays in their daily lives, or that they're rather uncommon.
My current theory is that by the time computers were sufficiently advanced to manipulate 45-bit segment displays, LCD-screens were already a thing and there was no longer a need for a segment display. Nevertheless, it surprises me that I cannot find an existing design.
Regardless, this is how my minimalist-but-readable design ended up. By just using 45 bits, this segment display can render every valid Hangul syllable block. It started as a way to learn the script more deeply, but it turned into a functional segment display that I hope to inspire some Korean tinkerers with.
You can try the live demo here. Feel free to mess with the design and make it your own. I won't be extending this design to Hanja (good luck cramming that into 45 bits!) but I'd love to keep in touch with anyone who builds onto this design.
Have fun.
#korea #segmentdisplay
Older English post <<<
Older post <<< >>> Newer post